Introduction to Machine Learning
This introduction has been adapted from Borja’s PhD thesis (Requena 2024).
1 What is machine learning?
With the progress of technology, we encounter increasingly more complex and abstract problems that are hard to formalize mathematically. For instance, the problem of face recognition in images cannot be easily presented in a formal mathematical way, or tasks such as detecting new phases of matter may not even have a known mathematical formulation. Hence, these types of problems cannot be effectively addressed using standard hard-coded algorithms.
The field of machine learning (ML) emerges as a new paradigm to develop algorithms that are not explicitly programmed, but learned from experience instead, typically in the form of data. Figure 1 provides a visual comparison between traditional programming and ML. In traditional programming, an input task and a program to solve it yield the desired result after some computation. In ML, an input task and related data instances result in a program to solve the task. For example, the data can be pairs of problem examples and their solutions.
This process heavily relies on applied statistics, emphasizing the use of computers to approximate complex functions. Deep learning (Goodfellow, Bengio, and Courville 2016), a subfield of ML, is the maximum exponent of this trend. It employs parametrized hierarchical models to extract intricate patterns from data, achieving outstanding results across various tasks.

In short, an ML algorithm is an algorithm capable of learning from data. We can consider a computer program to learn from experience with respect to some class of tasks and performance measure if its performance in those tasks improves with experience (Mitchell 1997). Hence, there are a few fundamental ingredients to any learning algorithm:
- A task to solve: Tasks are often defined in terms of how examples or data instances should be processed. These are usually represented by vectors \(\mathbf{x}\in\mathbb{R}^n\) where every entry is a feature. We show some typical ML tasks in the applications chapter.
- A performance measure: A consistent quantitative measure of the ML algorithm’s performance on the task. These metrics can range from simple direct comparisons between the obtained and expected output, to more involved and task-specific functions.
- Data (experience): A data set containing a collection of data instances, potentially including the desired output \(\mathbf{y}\) for each of them \(\{(\mathbf{x}_i,\mathbf{y}_i)\}\). We consider different types of learning depending on the kind of data set the algorithm is allowed to experience, as detailed in the types of learning section below.
- A model: The structure that encodes the resulting program. This can range from a parametrized linear function, to a combination of deep neural networks.
In these terms, the learning process can be described as the iterative maximization of the model’s performance on the given task and data.
2 Machine learning tasks
The main ingredient in the learning process is a task. It is important to distinguish the objective task with the learning process itself. The latter is the process through which the ability to develop the task is acquired. For example, if we would like a robot to walk, walking is the task (Goodfellow, Bengio, and Courville 2016).
There are very diverse tasks that can be solved with ML. The most common ones are regression and classification tasks. In regression tasks, we typically assume a relationship between two variables of the form \(\mathbf{y}=f(\mathbf{x})\). In general, the two variables can be multi-dimensional, and the objective is to find the function \(f\) that relates them. In classification tasks, the objective is to learn a function \(f\) that assigns an input \(\mathbf{x}\) to a certain category or label \(y\) among a finite set of labels. Unlike in regression tasks, these categories do not need to have a numerical meaning and we typically assign them an integer index to encode them.
We show some examples in the machine learning application overview section, and cover even more throughout the entire course!
3 Types of learning
A crucial factor in the learning process is data, and its accessibility often determines the types of learning we can consider. The notions of task and data are intertwined: certain tasks can only be solved if sufficient data is available, and richer data enables the seamless transition between tasks. In the ML field, we typically refer to data in terms of a data set \(\mathcal{D}\), containing a finite amount of data instances often called data points or examples \(\mathbf{x}_i\). The data set may exclusively contain the data instances, \(\mathcal{D} = \{\mathbf{x}_i\}\), or they may also be accompanied by predefined labels or targets \(\mathbf{y}_i\), forming tuples \(\mathcal{D} = \{(\mathbf{x}_i,\mathbf{y}_i)\}\). In some cases, the data points can be organized into a design matrix \(\mathbf{X}\), formed by stacking \(\{\mathbf{x}_i\}\) either row- or column-wise.
Each element of every data point \(\mathbf{x}_i\) is known as a feature, and it is a descriptor of a specific aspect of the example. Selecting the right features to characterize the object of interest can be challenging: too few might fail to capture all relevant aspects, whereas too many can lead to spurious correlations that interfere with the conclusions drawn from the data. Additionally, the data can be arbitrarily processed and transformed, for instance, subtracting the mean of every feature across the data set \(\mathcal{D}\) from each data point prior to any further analysis. Determining the right data representation is a central problem in ML, as it is essential to perform any task, and it is the core of the field of representation learning.
In general, the type of available data effectively defines the types of learning our model can be faced with. These are usually divided into three categories: supervised, unsupervised, and reinforcement learning.
3.1 Supervised learning
Supervised learning refers to ML algorithms that learn from labeled data \(\mathcal{D} = \{(\mathbf{x}_i,\mathbf{y}_i)\}\). There exist various approaches to supervised learning, spanning from statistical methods to classical ML and deep learning. In most cases, substantial amounts of data are required for the training process, which entails the accurate labeling of the data. This is usually considered one of the most significant drawbacks of supervised learning, as obtaining perfectly matched labels is not always feasible or may require extensive manual annotation by humans.
3.2 Unsupervised learning
While labeled data may be scarce, we often have access to large amounts of raw unlabeled data \(\mathcal{D} = \{\mathbf{x}_i\}\). In this case, we can employ unsupervised learning, which refers to ML algorithms that learn from unlabeled data. Unsupervised learning can either be used for preliminary pre-processing steps, such as dimensionality reduction, or for representation learning, as in data clustering. Furthermore, it can be used to learn the underlying probability distribution of the data and generate entirely new examples.
3.3 Reinforcement learning
In contrast to the two previous types of learning, some ML do not rely on a fixed data set \(\mathcal{D}\). For instance, in reinforcement learning, we usually do not even have a data set at all from the beginning. Instead, the learning algorithm interacts with an environment in a feedback loop to accomplish a given task. The data set is gradually shaped as the learning system collects experiences derived from these interactions. Different reinforcement learning algorithms manage the collected data differently, although it is always leveraged to achieve the objective task.
4 Learning as an optimization task
The model encodes the structure of the resulting program, and it is typically a function of the data, \(f(\mathbf{x})\), whose output depends on the task. For example, the output can be a class from a discrete set of possible classes in a classification task, or a complex-valued tensor in a regression task. Finding the function that provides the best mapping between the data and the desired outcome for a specific task is at the heart of ML. The model is usually characterized by a set of parameters \(\mathbf{\theta}\), and all its possible parametrizations form the set of functions known as the hypothesis space.
The performance measure objectively quantifies the model’s performance in a given task. For example, in a classification task, we may consider the accuracy, which is the proportion of examples for which the model outputs the correct result. We can obtain the same information with the error rate, which is the proportion of missclassified examples. In a regression task, we may consider the squared difference between the model’s output and the desired value averaged over all data points, known as the mean squared error (MSE).
We distinguish between metrics and loss functions. The former are performance measures that provide valuable information but may not be smooth, such as the accuracy. Conversely, the latter may not be as informative, but they are always differentiable. Typically, loss functions quantify the errors performed by the model such that smaller losses translate into better models.
For example, in a regression task we may consider the the MSE as loss function, which is defined as: \[\begin{equation} \mathcal{L}_{\text{MSE}} = \frac{1}{n}\sum_i^n\left(y_i-f(\mathbf{x}_i)\right)^2\,, \end{equation}\] where \(n\) is the size of the data set and \(y_i\) is the expected value for each sample \(\mathbf{x}_i\). For a classificationt task, we may use the cross-entropy loss function: \[\begin{equation} \mathcal{L}_{\text{CE}} = -\frac{1}{n}\sum_i^n \mathbf{y}_i^T\log(f(\mathbf{x}_i))\,. \end{equation}\] In these cases, \(f(\mathbf{x}_i)\) is a vector containing the probability that the data point \(\mathbf{x}_i\) belongs to each of the possible classes, and \(\mathbf{y}_i\) is the vector of the true class, e.g., \(\mathbf{y}_i=\left[0, 0, 1, 0\right]^T\) encodes the third class in a four-class classification problem. The absolute value of \(\mathcal{L}_{\text{CE}}\) does not provide a clear idea of the model’s performance, unlike the accuracy, but it is a smooth function in its domain.
Machines ``learn’’ by minimizing the loss function \(\mathcal{L}\), over the training data set, i.e., the data available during the learning process. Formally, the objective is to find the optimal model parameters \(\mathbf{\theta}^*\) in the hypothesis space that minimize \(\mathcal{L}\). The minimization is usually performed by gradient-based techniques, hence the emphasis on the differentiability of \(\mathcal{L}\). Therefore, learning becomes an optimization process.
5 Capacity, overfitting and underfitting
The central challenge in ML is to ensure the model can generalize well. This means the resulting model should perform effectively on new data, never seen during the learning process. While learning, also known as training, our algorithm has access to the training data, as briefly introduced in the previous section. This allows us to quantify the performance over the so-called training set, obtaining a training error. To assess the generalization capabilities of the model, we hold out some data from the training process, forming a test set, and measuring the performance on this previously unseen data. This provides a test or generalization error. What distinguishes ML from mere function fitting is that the goal in ML is to keep both the training and test errors low, ensuring the proper generalization of the model.
Given that the parameter optimization of our model is performed in the training set, the expected test error is higher or equal than the expected training error. Their difference is known as the generalization gap, and it persists even when the training and test data are generated by identical probability distributions. Indeed, it may only disappear in the limit of infinite data. Hence, the overall performance of an ML model can be evaluated considering two factors: the training error and the generalization gap, which should both be as small as possible.
These two factors are related to two main challenges of ML: overfitting and underfitting. In short, underfitting occurs whenever the training error is not low enough, meaning that the model is unable to successfully develop the task. Overfitting is characterized by a large generalization gap, which is often the result of a low training error combined with a high test error. In these cases, the generalization is hindered by the model learning the specific details of the training data, rather than capturing the main patterns. Figure 2 shows a schematic depiction of both phenomena.
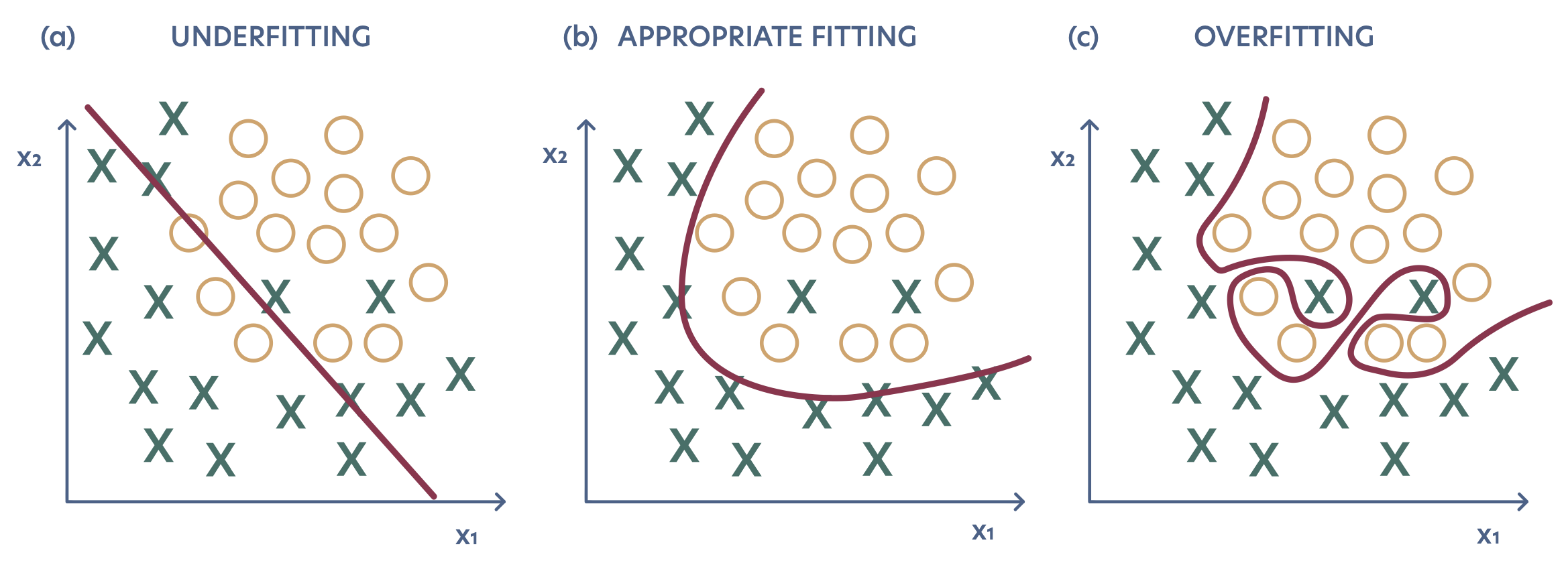
The tendency of the model to under- or overfit can be tuned by changing the model’s capacity. The capacity can be loosely understood as the measure of a model’s ability to fit a wide variety of functions (Goodfellow, Bengio, and Courville 2016). Models with low capacity may be unable to fit the training set, resulting in underfitting. On the other hand, models with a capacity much higher than required for the task tend to overfit, typically adjusting to the particularities of the training set, which may not be true for the general distribution. The challenge is to find the capacity that is ``just right’’ for the task.
To address this challenge, the data set can be further split to include a validation set, resulting in three subsets: training, validation and test sets. The validation set serves as pseudo-test set to evaluate the model’s generalization capabilities and adjust its hyper-parameters, which may impact its capacity. For example, the capacity can be controlled by constraining the model’s hypothesis space. In the case of a linear regression model, the hypothesis space contains all linear functions. Generalizing the linear model to include polynomial functions up to the \(k\)-th degree effectively increases its capacity, as shown in the linear models section. Adjusting the maximum polynomial degree allows the fine-tuning of the model’s capacity. In a deep learning architectures, the capacity can be adjusted by tuning the number of neurons and their connections.
Hence, the model learns from the data in the training set, and its hyper-parameters are tuned based on the generalization gap between the training and validation sets. This process may involve multiple training iterations as the model is being adjusted. Finally, the model’s performance is evaluated in the test, providing a real measure of its performance on unseen data.