a, b = 1.5, 1
x, y = noisy_line(a, b, noise=[0,2])Linear regression
1 The task
In this introductory notebook, we discuss our first learning algorithm to perform a regression task. Given a dataset \(\{\mathbf{x},\mathbf{y}\}\) of \(n\) points, we would like to find the line \(y'=\mathbf{w}^{T} \mathbf{x} + \mathbf{b}\) that best fits the data. Therefore, let us start by generating such a dataset for the one dimnesional case. We do so by taking the line \(y=ax+b\) and adding gaussian noise to \(y\). We have prepared a small package lectures_ml with functionalities to do these tasks easily.
You can access the documentation of any function by pressing the tab key or by adding a ? after the function. You can also see the source code by adding ?? after the function. If you want them to appear in a cell of the notebook, you can use the function nbdev.showdoc() for the documentation and lectures_ml.utils.show_code().
Figure 1 shows the dataset \(\{x,y\}\). As expected, the dataset follows the linear relation dispersion (in red) but with some noise.
Code
fig = go.Figure()
fig.add_scatter(x=x, y=y, mode="markers", name='data',
hovertemplate='x:%{x:.2f}'
+'<br>y:%{y:.2f}</br><extra></extra>')
x1 = np.array([x.min(),x.max()])
y1 = a*x1+b
fig.add_scatter(x=x1, y=y1, mode="lines",name='Ground Truth')
fig.update_layout(width=800,height=400,xaxis={'title':'x'},yaxis={'title':'y'})
fig.show()2 Learning as an optimization problem
The goal of the learning task is to find the slope and the intercept of the line directly from the data. Therefore, we have to define a suitable model to solve the task with the given data. In general, the model is a function of the input data, \(f(\mathbf{x})\), whose output is interpreted as a prediction for the input data. We start by declaring a certain parametrization of a model (function), e.g., \(f(\mathbf{x}) = \mathbf{w}^{T} \mathbf{x} + \mathbf{b}\), with \(\theta \supset \{\mathbf{w}, \mathbf{b}\}\) denoting the model parameters. Then, all possible parametrizations of this function form the set of functions, i.e., the hypothesis class.
Machines ‘’learn’’ by minimizing a loss function of the training data, i.e., all the data accessible to the ML model during the learning process. The minimization is done by tuning the parameters of the model. We need to choose the loss function according to the objective task, although there is certain freedom on how to do it. In general, the loss function compares the model predictions or a developed solution against the reality or expectations. Therefore, learning becomes an optimization problem.
Here, we use the terms of loss, error, and cost functions 1 interchangeably following Ref. (Goodfellow, Bengio, and Courville 2016). Popular examples of loss functions include the mean square error and the cross entropy, used for supervised regression and classification 2 problems.
3 The loss function: Mean square error
Having a model, we now have to define a loss function for our regression task. For this case, we choose the mean square error, defined as \[MSE=\frac{1}{N}\sum_{i=1}^{N}(y_i'-y_i)^2.\] Such a loss measures the mean vertical distance between the dataset and the line \(y'=ax+b\) (see Figure 2).
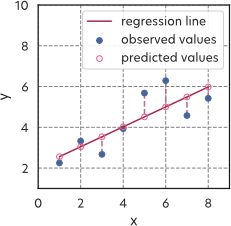
There is not a unique loss function suitable for our task. We could have chosen other losses such as, e.g., the Mean Absolute Error (MAE) or the Root Mean Squared Error (RMSE). The choice of the loss really depends on the problem and the dataset. As we will see later in the lecture, if the noise on the data is assumed to be gaussian (which is our case), the mean square error is the most natural choice.
Let us now study the loss function in terms of its two variables \(a\) and \(b\) for our dataset \(\{x,y\}\). Figure 3 shows the contour plot of the logarithm of loss function in terms of \(a\) and \(b\). We can clearly see that the minimum appears at the expected values of the line we generated in the previous section.
Code generating the data of the figure
vec_a = np.arange(-5,5,0.1)
vec_b = np.arange(-5,5,0.1)
matz, matzg = np.zeros((vec_a.size,vec_b.size)), np.zeros((vec_a.size,vec_b.size,2))
vec = np.zeros((vec_a.size*vec_b.size,3))
for i, a1 in enumerate(vec_a):
for j, b1 in enumerate(vec_b):
matz[i,j] = MSE(x,y,lambda x:a1*x+b1)
matzg[i,j,:] = grad_MSE_lr(x,y,dict(a=a1,b=b1))Code
fig = go.Figure()
fig.add_contour(z=np.log(matz),x=vec_b, y=vec_a,hovertemplate=
'a:%{y:.2f}'
+'<br>b:%{x:.2f}</br>'
+'f:%{z:.2f}<extra></extra>')
fig.add_scatter(x=[b],y=[a], marker_color='White')
d = dict(width=600,
height=600,
xaxis={'title':'b'},
yaxis={'title':'a'}
)
fig.update_layout(d)
fig.show()4 Finding the minimum of the loss function
In the case of the mean square error, we can derive analytically the optimal values of \(a\) and \(b\). To this end, we start by writing the gradients \[ \begin{align} &\partial_a MSE=\frac{2}{N}\sum_{i=1}^{N}(y_i'-y_i)x_i\\ &\partial_b MSE=\frac{2}{N}\sum_{i=1}^{N}(y_i'-y_i). \end{align} \]
This leads to the linear system of equations for \(a\) and \(b\) when the gradients vanish \[ \begin{align} &a \sum_{i=1}^N x_i^2+b \sum_{i=1}^N x_i - \sum_{i=1}^N y_i x_i =0\\ &a \sum_{i=1}^N x_i+b N -\sum_{i=1}^N y_i =0 \end{align} \]
We can easily solve this system of equation to find
\[ \begin{align} & b = \bar{y} - a \bar{x}\\ & a = \frac{\sum_{i=1}^N (x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^N(x_i-\bar{x})^2}, \end{align} \] where \(\bar{x}\) (\(\bar{y}\)) stands for the mean of \(x\) (\(y\)). As this problem is convex, we have found the unique global minimum.
Implement a function linear_regression_analytic(x,y) to compute the analytical optimal values for the slope and intercept given a dataset with samples x and y, such as the one we have created above.
Code
def linear_regression_analytic(x,y):
xb, yb = np.mean(x), np.mean(y)
a = np.sum((x-xb)*(y-yb))/np.sum((x-xb)**2)
b = yb - a*xb
return a,bestimate_a, estimate_b = linear_regression_analytic(x,y)
print(f'a={estimate_a:.3f}\nb={estimate_b:.3f}')a=1.485
b=0.955We have just performed our first learning task!
5 Gradient Descent
In general, we do not have a tractable closed expression for the optimal parameters and we need to solve the optimization task through other means. Here, we introduce gradient-based approaches, which, despite not being needed for this task, it will allow us to introduce important concepts that will appear in a more abstract form in neural networks.
Let us first study the gradients. Figure 4 shows the gradients of the MSE with respect to \(a\) and \(b\). The values of \(a\) and \(b\) of the line lie in the zero contour lines of the gradients.
Code
for i in range(2):
mat = matzg[:,:,i]
fig = go.Figure()
fig.add_contour(z=mat,x=vec_b, y=vec_a)
fig.add_contour(z=mat,x=vec_b, y=vec_a)
fig.add_scatter(x=[b],y=[a], marker_color='White')
d = dict(
xaxis={'title':'b'},
yaxis={'title':'a'}
)
fig.update_layout(d)
fig.show()We can now perform a gradient optimization. The simplest one is the gradient descent algorithm (often called steepest descent algorithm). This iterative algorithms works as follows:
Let us first see how the algorithm works over a very simple function \(f(x)=x^2\). This convex function has a unique global minimum at \(x=0\) and we can compute its gradient analitically.
def f(x): return x**2
def grad_f(x): return 2*xWe then choose an initial strating point \(x_0\) and perform n_iter iterations of the gradient descent algorithm.
n_iter = 20
vecx = np.zeros(n_iter+1)
vecf = np.zeros(n_iter+1)
eta = 1E-1
x0 = 2
vecx[0] = x0
vecf[0] = f(x0)
for i in np.arange(n_iter):
vecx[i+1] = vecx[i] - eta* grad_f(vecx[i])
vecf[i+1] = f(vecx[i+1])Code
fig = go.Figure()
x1 = np.arange(-2.5,2.51,0.01)
y1 = x1**2
fig.add_scatter(x=x1, y=y1, mode="lines",name='Parabola',marker_color='#EF553B')
fig.add_scatter(x=vecx, y=vecf, mode="markers", name='GD',
hovertemplate='x:%{x:.2f}'
+'<br>y:%{y:.2f}</br><extra></extra>',marker_color='#636EFA',marker_size=8)
fig.update_layout(width=800,height=400,xaxis={'title':'x'},yaxis={'title':'f(x)'})
fig.show()Figure 5 shows a nice convergence of the algorithm to the global minimum \(x=0\).
For such convex cases, the gradient descent algorithm is guaranteed to converge to the global minimum for sufficiently small \(\eta\). For non-convex problems, it allows us to reach a local minimum with no guarantee that it is the global one. Indeed, in practice, we hardly ever reach the global optimum, but it is usually sufficient to reach a local one that is close enough.
Let us now come back to our linear regression problem. We consider n_ini random initial values for our parameters and run the gradient descent algortihm. Rather than writing the whole algorithm again, we use the gradient_descent function from the lectures_ml library.
n_ini = 5
veca0, vecb0 = np.random.uniform(low=vec_a[1], high=vec_a[-2], size=n_ini),np.random.uniform(low=vec_b[1], high=vec_b[-2], size=n_ini)
ll = dict(loss=MSE, grads=grad_MSE_lr, fun=line)
df = pd.DataFrame(columns=['a','b','label','value'])
for i in range(n_ini):
pini = dict(a=veca0[i],b=vecb0[i])
trackers = gradient_descent(x, y, pini, ll, niter=int(1E4), eta=1E-3)
df1 = pd.DataFrame(data={'a':trackers['a'],'b':trackers['b'],'label':f'traj {i+1}','value':trackers['loss']})
df = pd.concat([df, df1])Figure 6 depicts the loss functions in terms of the epochs for the different trajectories. The initial value of the loss function strongly varies depending on the initial conditions.However, we observe that the steepest descent algorithm drives rapidly the parameters towards the minimum.
Code
fig = px.scatter(df, y='value',animation_frame='label')
fig["layout"].pop("updatemenus") # optional, drop animation buttons
fig.update_layout(xaxis_title='epochs',yaxis_title='Loss')
fig.show()Figure 7 shows the trajectories in the parameter space.
Code
fig = go.Figure()
fig.add_contour(z=np.log(matz),x=vec_b, y=vec_a,
hovertemplate=
'a:%{y:.2f}'
+'<br>b:%{x:.2f}</br>'
+'f:%{z:.2f}<extra></extra>')
hovertemplate ='a:%{a}'+'b:%{b}<extra></extra>'
for i in range(n_ini):
visible = True if i == 0 else 'legendonly'
newdf = df[df.label == f'traj {i+1}']
fig.add_scatter(x=newdf.b, y=newdf.a, name=f'traj {i+1}',text=newdf.value,
hovertemplate=
'a:%{y:.2f}'
+'<br>b:%{x:.2f}</br>'
+'f:%{text:.2f}<extra></extra>', visible=visible)
legend=dict(
yanchor="top",
y=1.3,
xanchor="left",
x=0.1
)
d = dict(width=800,
height=600,
xaxis={'title':'b'},
yaxis={'title':'a'},
legend = legend
)
fig.update_layout(d)
fig.show()6 Choosing a Learning rate
Choosing a learning rate has an impact on convergence to the minimum, as depicted in Figure 8.
- If the learning rate is too small, the training needs many epochs.
- The right learning rate allows for a fast convergence to a minimum and needs to be found.
- If the learning rate is too large, optimization can take you away from the minimum (you ``overshoot’’).
Let us first illustrate the latter on the parabola example.
treshold = 1E-6
imax = int(1E4)
x0 = 2
eta = 1E-3
vecx, vecf = [x0], [f(x0)]
x1=x0
i = 0
dl = 10
while dl>treshold and i<imax:
i = i+1
x1 = x1 - eta* grad_f(x1)
vecx.append(x1)
vecf.append(f(x1))
dl = np.abs(vecf[-1]-vecf[-2])
if vecf[-1]>1000.: breakCode
fig = go.Figure()
x1 = np.arange(-2.5,2.51,0.01)
y1 = x1**2
fig.add_scatter(x=x1, y=y1, mode="lines",name='Parabola',marker_color='#EF553B')
fig.add_scatter(x=vecx, y=vecf, mode="lines+markers", name='GD',
hovertemplate='x:%{x:.2f}'
+'<br>y:%{y:.2f}</br><extra></extra>',marker_color='#636EFA',marker_size=8)
fig.update_layout(width=800,height=400,xaxis={'title':'x'},yaxis={'title':'f(x)'},title=f'number of iterations to reach the threshold {treshold:.0e}: {i}')
fig.show()Rerun the last experiment for \(\eta=10^{-3},10^{-1},1.1\). What do you see?
We now perform a similar analysis for the linear regression problem. To this end, we choose a vector of learning rates vec_eta for the same initial condition and we apply the steepest descent algorithm.
vec_eta = [1E-4,1E-3,1E-2,2E-2,3E-2,5E-2,1E-1]
n_ini = len(vec_eta)
pini = dict(a=-1.8, b=1)
df = pd.DataFrame(columns=['a','b','label','value'])
for i in range(n_ini):
trackers = gradient_descent(x, y, pini, ll, niter=int(1E4),eta=vec_eta[i])
df1 = pd.DataFrame(data={'a':trackers['a'],'b':trackers['b'],'label':f'traj {i+1}','eta':vec_eta[i],'value':trackers['loss']})
df = pd.concat([df, df1])Code
fig = go.Figure()
fig.add_contour(z=np.log(matz),x=vec_b, y=vec_a,
hovertemplate=
'a:%{y:.2f}'
+'<br>b:%{x:.2f}</br>'
+'f:%{z:.2f}<extra></extra>')
hovertemplate ='a:%{a}'+'b:%{b}<extra></extra>'
for i in range(n_ini):
visible = True if i == 0 else 'legendonly'
newdf = df[df.label == f'traj {i+1}']
fig.add_scatter(x=newdf.b, y=newdf.a, name=f'eta = {vec_eta[i]}',text=newdf.value,
hovertemplate=
'a:%{y:.2f}'
+'<br>b:%{x:.2f}</br>'
+'f:%{text:.2f}<extra></extra>',
visible=visible)
legend=dict(
yanchor="top",
y=1.3,
xanchor="left",
x=0.01
)
d = dict(width=800,
height=600,
xaxis={'title':'b'},
yaxis={'title':'a'},
legend = legend,
xaxis_range=[vec_b[1], vec_b[-1]],
yaxis_range=[vec_a[1], vec_a[-1]]
)
fig.update_layout(d)
fig.show()7 Stochastic Gradient Descent
The gradient descent algorithm requires to pass through the whole training set to compute the gradient. However, in some cases, this can be quite costly. Imagine, for example, the case of linear regression with many variables and many training examples. To overcome this limitation, computer scientists have designed a stochastic alternative to gradient descent: the stochastic gradient descent (SGD).
While stochastic gradient descent is not very relevant for the case of the linear regression with two parameters, it will become very important in the case of neural networks. We here take the simplicity of the loss landscape of such model to illustrate the main properties of stochastic gradient descent.
The main idea behind stochastic gradient descent is to approximate the loss function of the training set by the gradient of a single training sample. While, each gradient step is a relatively bad approximation, the random walk followed by the aglorithm eventually converges to the direction of the steepest descent. This can be intuitively seen by noting that the mean of the gradient of several training points is pointing towards the steepest descent. The algorihtm for each epoch is sketched in the next box.
We now have two extreme cases: the gradient descent algorithm with no stochasticiy and the stochastic gradient descent with full stochasticity. This version of the stochastic gradient descent can be very unstable and take extremely long times to converge. Thus, it is desirable to find a middle ground: minibacth gradient descent. In this case, rather than taking the gradient over a single training example, we consider \(n_\text{batch}\) training samples in the stochastic gradient descent loop. This way, we obtain a better estimate of the gradient while preserving some of its stochasticity.
We illustrate the stochastic gradient descent with the follwoing code snippet for the same initial condition and for a minibatch of size n_batch=20.
n_ini = 5
pini = dict(a=2, b=1)
df = pd.DataFrame(columns=['a','b','label','value','niter'])
trackers = gradient_descent(x, y, pini, ll, niter=int(1E3))
df1 = pd.DataFrame(data={'a':trackers['a'],'b':trackers['b'],'label':f'GD','value':trackers['loss'],'niter':np.arange(len(trackers['a']))})
df = pd.concat([df, df1])
for i in range(n_ini):
trackers = sgd(x,y, pini, ll, niter=int(1E2))
df1 = pd.DataFrame(data={'a':trackers['a'],'b':trackers['b'],'niter':np.arange(len(trackers['a'])),'label':f'traj {i+1}','value':trackers['loss']})
df = pd.concat([df, df1])Code
fig = px.line(df, y='value', markers=True, animation_frame='label')
fig["layout"].pop("updatemenus") # optional, drop animation buttons
fig.update_layout(xaxis_title='iterations', yaxis_title='Loss')
fig.show()Figure 11 depcits the loss function of the gradient descent and the stochastic gradient descent algorithm for different shufflings. While both algorithms converge to a similar value of the Loss function, we can nicely observe the fluctuations coming from the stochasticity of the minibatches3. The latter can be also seen in Figure 12. It is interesting to notice in that last figure that the stochastic gradient descent fuctuates more in the \(a\)-direction. This fact is well known for SGD and can be improved with more avolved algorithms such as momentum, nesterov or Adam.
Code
amin, amax = df.a.min()*0.8,df.a.max()*1.1
bmin, bmax = df.b.min()*0.8,df.b.max()*1.1
n = 100
vec_a = np.arange(amin, amax,(amax-amin)/n)
vec_b = np.arange(bmin, bmax,(bmax-bmin)/n)
matz = np.zeros((vec_a.size,vec_b.size))
for i, a1 in enumerate(vec_a):
for j, b1 in enumerate(vec_b):
params = dict(a=a1, b=b1)
matz[i,j] = MSE(x,y,line,params)
fig = go.Figure()
fig.add_contour(z=np.log(matz),x=vec_b, y=vec_a,
hovertemplate=
'a:%{y:.2f}'
+'<br>b:%{x:.2f}</br>'
+'f:%{z:.2f}<extra></extra>')
hovertemplate ='a:%{a}'+'b:%{b}<extra></extra>'
for i in range(n_ini):
visible = True if i == 0 else 'legendonly'
newdf = df[df.label == f'traj {i+1}']
fig.add_scatter(x=newdf.b, y=newdf.a, name=f'traj {i+1}',text=newdf.value, mode='lines+markers',
hovertemplate=
'a:%{y:.2f}'
+'<br>b:%{x:.2f}</br>'
+'f:%{text:.2f}<extra></extra>',
visible=visible)
newdf = df[df.label == f'GD']
fig.add_scatter(x=newdf.b, y=newdf.a, name=f'GD',text=newdf.value,
mode='lines', line={'dash': 'dash','color':'White'},
hovertemplate=
'a:%{y:.2f}'
+'<br>b:%{x:.2f}</br>'
+'f:%{text:}<extra></extra>')
legend=dict(
yanchor="top",
y=1.3,
xanchor="left",
x=0.01
)
d = dict(width=800,
height=600,
xaxis={'title':'b'},
yaxis={'title':'a'},
legend = legend
)
fig.update_layout(d)
fig.show()Rerun the last experiment with different minibatch sizes. What do you see?
We finish this section by observing how the line adjust to our dataset in terms of the iterations for the GD and SGD. The results are presented in Figure 13 for the gradient descent.
Code generating the data of the figure
i =1
label = 'GD'#f'traj {i+1}' #change it if you want to see the SGD trajectory
x1 = np.array([x.min(),x.max()])
newdf = df[df.label == label]
a, b, mse = newdf.a.to_numpy(), newdf.b.to_numpy(), newdf.value.to_numpy()
y1 = np.einsum('i,j->ij',a,x1)+np.tile(b,(2,1)).TCode
frames = [go.Frame(data=[go.Scatter(x=x1, y=y1[i,:],mode='lines')],layout=go.Layout(title_text=f'step:{i}, MSE:{mse[i]:.2f}')) for i in range(a.size)]
buttons = [dict(label="Play",method="animate",
args=[None, {"frame": {"duration": 100, "redraw": True},
"fromcurrent": True,
"transition": {"duration": 300,"easing": "quadratic-in-out"}}]),
dict(label="Pause",method="animate",
args=[[None], {"frame": {"duration": 0, "redraw": False},"mode": "immediate","transition": {"duration": 0}}]),
dict(label="Restart",method="animate",
args=[None])]
Fig = go.Figure(
data=[go.Scatter(x=x1, y= y1[0,:],mode='lines',name = 'line'),
go.Scatter(x=x, y=y, mode="markers", name='data',
hovertemplate='x:%{x:.2f}'
+'<br>y:%{y:.2f}</br><extra></extra>')],
layout=go.Layout(
xaxis=dict(range=[x.min()-2, x.max()+2], autorange=False),
yaxis=dict(range=[y.min()-2, y.max()+2], autorange=False),
updatemenus=[dict(
type="buttons",
buttons=buttons)]
),
frames= frames
)
Fig.show()References
Footnotes
The literature also uses the terms of criterion or cost, error, or objective functions. Their definitions are not very strict. Following (Goodfellow, Bengio, and Courville 2016): ‘’The function we want to minimize or maximize is called the objective function, or criterion. When we are minimizing it, we may also call it the cost function, loss function, or error function. In this book, we use these terms interchangeably, though some machine learning publications assign special meaning to some of these term’’. For example, loss function may be defined for a single data point, the cost or error function may be a sum of loss functions, so check the definitions used in each paper.↩︎
For classification, a~more intuitive measure of the performance could be, e.g., accuracy, which is the ratio between the number of correctly classified examples and the data set size. Note, however, that gradient-based optimization requires measures of performance that are smooth and differentiable. These conditions distinguish loss functions from evaluation metrics such as accuracy, recall, precision, etc.↩︎
Beware that the notion of iteration is different for gradient descent and for stochastic gradient descent. For the former, an iteration corresponds to an epoch (the whole training set), while for the latter it corresponds to a minibatch.↩︎